Profile Image

Adam Thorpe

I am a postdoctoral researcher at the Oden Institute for Computational Engineering & Science at the University of Texas at Austin, working with Ufuk Topcu. I received my Ph.D. in 2023 from the University of New Mexico, advised by Meeko Oishi. I am broadly interested in topics related to data-driven methods for control, computational engineering, and human-centered autonomy.

adam.thorpe@ignore.meaustin.utexas.edu

Scholar GitHub CV

Research

I develop theory and algorithms for autonomy, robotics, control, and engineering that are adaptable, principled, and reliable. My research provides data-driven control algorithms based in the theory of Hilbert spaces that have quantifiable guarantees. By integrating neural network architectures with structured Hilbert space representations, I have developed principled methods for operator learning and techniques for zero-shot modeling of dynamical systems that are adaptable to new systems using only a few seconds of online data. Using statistical approaches rooted in functional analysis, I developed techniques for characterizing human-autonomy interactions to ultimately design autonomy that is responsive to individual needs and preferences.

Function Encoders for Zero Shot Robotics

We develop algorithms that enable robots to learn and adapt on the fly when they encounter something new. Rather than rely on fixed models, our approach lets robots adjust their behavior in real time as conditions change.

I led a project to design a new class of machine learning algorithms that can model entire families of robot dynamics and control policies. The method combines function encoders and neural ordinary differential equations (ODEs) to learn structured representations of dynamical systems that can be updated online in seconds.

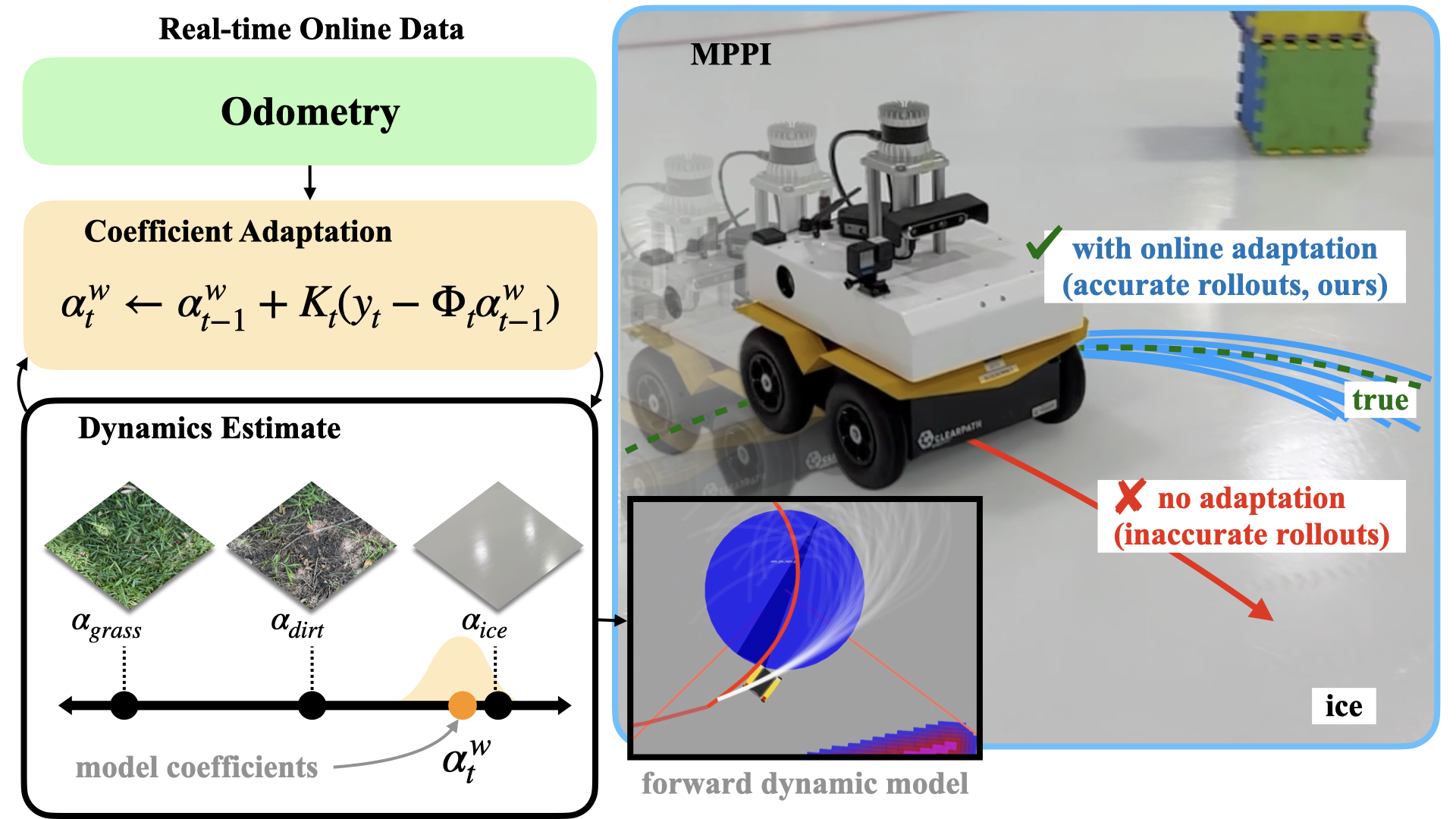
We demonstrated this through terrain adaptation, where robots learned to adapt their dynamics to new surfaces during operation. We even took our system to a local ice rink in Texas and taught it to drift on ice. Ultimately, these algorithms could enable robots operating in remote, unstructured environments (such as on the Moon) to handle situations that cannot be planned for in advance.

arXiv Online Adaptation of Terrain-Aware Dynamics for Planning in Unstructured Environments
arXiv Zero-Shot Transfer of Neural ODEs
GitHub - ajthor/function-encoder: Function encoder implementation in PyTorch.

Basis to Basis (B2B) Operator Learning

We develop methods for operator learning by modeling operators as mappings between learned representations of function spaces. This reframes operator learning as a map between functions, rather than a learned transformation on a fixed mesh, allowing us to capture the structure of complex systems more naturally.

I developed basis-to-basis (B2B) operator learning, an approach that learns separate functional bases for the input and output spaces and then learns how to map between them. This decomposition makes it possible to approximate operators efficiently while preserving their functional relationships.

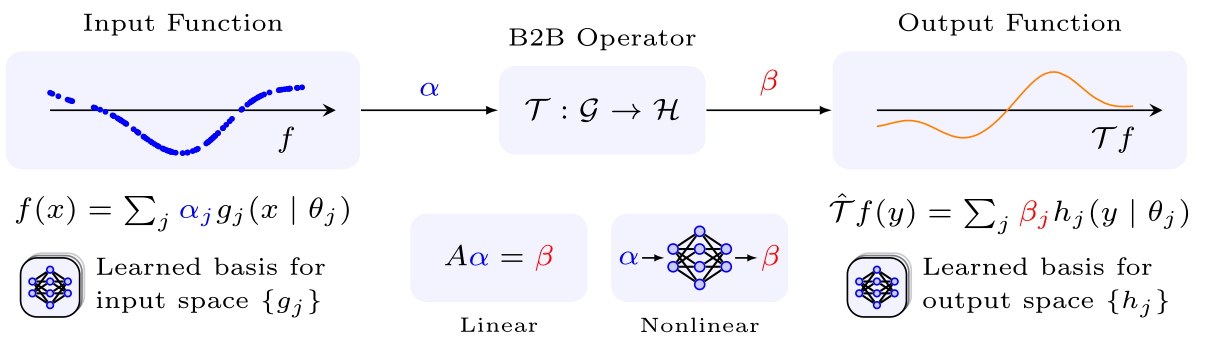
Traditional operator learning methods depend on discretized inputs, which limits their use in real-world autonomy. By learning in continuous function spaces, we achieve surrogate models that are compact, adaptive, and practical for embedded systems in robotics and autonomous control.

ScienceDirect Basis to Basis Operator Learning Using Function Encoders

Cognitive Autonomy for Human Centered Systems

We develop autonomy that adapts to people rather than expecting people to adapt to automation. This work was part of an NSF CPS Frontiers project on cognitive autonomy, which brought together control theory, human factors, and cognitive science to understand how humans and autonomous systems can learn from one another.

I developed new methods for modeling and personalizing human–autonomy interaction. A central idea in this work is that there is no universal model of human behavior; autonomy must recognize individual differences and adapt accordingly.

As part of this effort, we used functional near-infrared spectroscopy (fNIRS) to measure cognitive activation and developed dynamical models of cognitive state during a quadrotor piloting task. These models captured how attention and workload evolved over time and linked cognitive state changes to control performance. We also created statistical techniques for personalizing autonomy from limited human data, allowing systems to learn how individuals differ in their response to feedback and adapt their behavior accordingly.

We demonstrated these ideas through a personalized quadrotor training system that adjusted task difficulty and feedback based on each learner’s performance and engagement. This work moves toward autonomy that adapts to you as an individual, making intelligent systems more intuitive, safe, and responsive.

SAGE Assessing the Relationship Between Learning Stages and Prefrontal Cortex Activation in a Psychomotor Task
ACM Characterizing the Effect of Mind Wandering on Braking Dynamics in Partially Autonomous Vehicles
IEEE Using Reward Shaping to Train Cognitive-Based Control Policies for Intelligent Tutoring Systems

Kernel-Based Stochastic Optimal Control

I develop control algorithms that make reliable decisions under uncertainty without making any prior assumptions about the nature of the disturbance. In many real systems, especially those involving people, disturbances are non-Gaussian, unpredictable, and difficult to model. My work focuses on developing principled control algorithms that tackle the most complex stochastic optimal control problems, where the disturbance is completely unknown. These algorithms leverage tools from functional analysis to reason about uncertainty while maintaining formal guarantees on safety and performance.

I developed kernel-based methods for stochastic optimal control that reformulate problems like dynamic programming, chance-constrained optimization, and stochastic reachability directly in reproducing kernel Hilbert spaces. By embedding probability distributions as kernel mean embeddings, these methods capture the full structure of uncertainty, including non-Gaussian and heavy-tailed disturbances, without relying on parametric models.

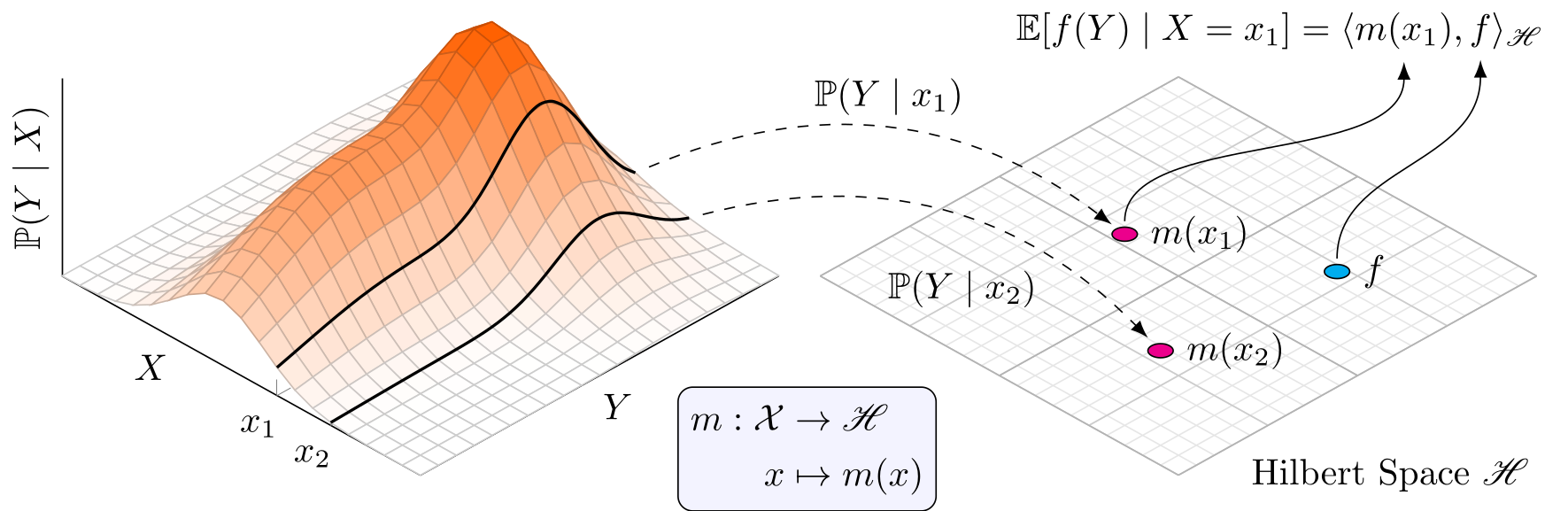
The resulting formulations can be solved efficiently as linear programs, allowing controllers to satisfy safety and performance guarantees even in stochastic environments. These techniques are especially powerful in domains where uncertainty is unavoidable and data are scarce, such as space robotics, human-centered autonomy, and safety-critical systems that must operate under unpredictable conditions.

IEEE Physics-Informed Kernel Embeddings: Integrating Prior System Knowledge with Data-Driven Control
IEEE Stochastic Optimal Control via Hilbert Space Embeddings of Distributions
arXiv Data-Driven Chance Constrained Control using Kernel Distribution Embeddings

Journal Articles

  1. T. Ingebrand, A. J. Thorpe, S. Goswami, K. Kumar, and U. Topcu, “Basis-to-basis operator learning using function encoders,” Computer Methods in Applied Mechanics and Engineering, 2025.
    Paper Code Project Page
  2. A. J. Thorpe, F. Djeumou, C. Neary, M. M. K. Oishi, and U. Topcu, “Physics-informed kernel embeddings: A unified approach to integrating prior knowledge of dynamics and system properties,” Transactions on Automatic Control, 2024, (Submitted).
  3. H. Sridhar, G. Huang, A. Thorpe, M. Oishi, and P. J. Brandon, “Characterizing the effect of mind wandering on braking dynamics in partially autonomous vehicles,” Transactions on Cyber-Physical Systems, 2023.
    Paper
  4. A. J. Thorpe, K. R. Ortiz, and M. M. K. Oishi, “State-based confidence bounds for data-driven stochastic reachability using Hilbert space embeddings,” Automatica, vol. 138, p. 110 146, 2022.
    Paper
  5. A. P. Vinod, A. J. Thorpe, P. A. Olaniyi, T. H. Summers, and M. M. K. Oishi, “Sensor selection for dynamics-driven user-interface design,” IEEE Transactions on Control Systems Technology, vol. 30, no. 1, pp. 71–84, 2022.
    Paper
  6. A. J. Thorpe and M. M. K. Oishi, “Model-free stochastic reachability using kernel distribution embeddings,” IEEE Control Systems Letters, vol. 4, no. 2, pp. 512–517, 2020.
    Paper

Conference Papers

  1. S. A. Low, Q. Rommel, K. S. Miller, A. J. Thorpe, U. Topcu, "Function Spaces Without Kernels: Learning Compact Hilbert Space Representations," (Submitted to ICLR 2026).
    Paper
  2. W. Ward, S. Etter, J. Quattrociocchi, C. Ellis, A. J. Thorpe, U. Topcu, "Zero to Autonomy in Real-Time: Online Adaptation of Dynamics in Unstructured Environments," (Submitted to ICRA 2026).
    Paper
  3. W. Ward, S. Etter, T. Ingebrand, C. Ellis, A. Thorpe, U. Topcu, "Online Adaptation of Terrain-Aware Dynamics for Planning in Unstructured Environments," RSS 2025 Workshop on Resilient Off-road Autonomous Robotics, 2025.
    Slides Paper Code
  4. T. Ingebrand, A. J. Thorpe, U. Topcu, "Function Encoders: A Principled Approach to Transfer Learning in Hilbert Spaces," International Conference on Machine Learning (ICML), 2025.
  5. A. J. Thorpe, T. Ingebrand, S. Goswami, K. Kumar, and U. Topcu, “Basis-to-basis operator learning: A paradigm for scalable and interpretable operator learning on Hilbert spaces,” in 2025 SIAM Conference on Computational Science and Engineering, 2025.
    Code Project Page Slides
  6. T. Ingebrand, A. J. Thorpe, and U. Topcu, “Zero-shot transfer of neural ODEs,” in Advances in Neural Information Processing Systems, 2024.
    Paper Code Project Page
  7. Y. Yu, A. J. Thorpe, J. Milzman, D. Fridovich-Keil, and U. Topcu, “Sensing resource allocation against data-poisoning attacks in traffic routing,” in 2024 63rd IEEE Conference on Decision and Control, 2024.
    Paper
  8. K. Ortiz, R. DiPirro, A. Thorpe, and M. Oishi, “Online learning of dynamical systems using low-rank updates to physics-informed kernel distribution embeddings,” in 2024 IEEE 63rd Conference on Decision and Control (CDC), Milan, Italy, 2024.
  9. M. S. Yuh, E. Rabb, A. Thorpe and N. Jain, "Using Reward Shaping to Train Cognitive-Based Control Policies for Intelligent Tutoring Systems," 2024 American Control Conference (ACC), Toronto, ON, Canada, 2024.
    Paper
  10. A. J. Thorpe, F. Djeumou, C. Neary, M. M. K. Oishi, and U. Topcu, “Physics-informed kernel embeddings: Integrating prior system knowledge with data-driven control,” in 2024 American Control Conference (ACC), 2024.
    Paper
  11. K. R. Ortiz, J. G. Hunter, A. J. Thorpe, et al., “Assessing the relationship between learning stages and prefrontal cortex activation in a psychomotor task,” Proceedings of the Human Factors and Ergonomics Society Annual Meeting, 2024.
    Paper
  12. K. S. Miller, A. J. Thorpe, and U. Topcu, “Active learning of dynamics using prior domain knowledge in the sampling process,” in 2024 63rd IEEE Conference on Decision and Control, 2024.
    Paper
  13. H. I. Khan, A. J. Thorpe, and D. Fridovich-Keil, “Act natural! projecting autonomous system trajectories into naturalistic behavior sets,” in IFAC Workshop on Cyber-Physical & Human Systems, 2024.
    Paper
  14. A. Thorpe, T. Lew, M. Oishi, and M. Pavone, “Data-driven chance constrained control using kernel distribution embeddings,” in Proceedings of The 4th Annual Learning for Dynamics and Control Conference, vol. 168, PMLR, 23–24 Jun 2022, pp. 790–802.
    Paper
  15. K. R. Ortiz, A. J. Thorpe, A. Perez, M. Luster, B. J. Pitts, and M. Oishi, “Characterizing within-driver variability in driving dynamics during obstacle avoidance maneuvers,” in IFAC Workshop on Cyber-Physical & Human Systems, 2022.
    Paper
  16. A. J. Thorpe and M. M. K. Oishi, “SOCKS: A stochastic optimal control and reachability toolbox using kernel methods,” in 25th ACM International Conference on Hybrid Systems: Computation and Control, ser. HSCC ’22, Milan, Italy: Association for Computing Machinery, 2022.
    Paper Code Project Page Video
  17. A. J. Thorpe, V. Sivaramakrishnan, and M. M. K. Oishi, “Approximate stochastic reachability for high dimensional systems,” in 2021 American Control Conference, 2021, pp. 1287–1293.
    Paper
  18. A. J. Thorpe, K. R. Ortiz, and M. M. K. Oishi, “SReachTools kernel module: Data-driven stochastic reachability using Hilbert space embeddings of distributions,” in 2021 60th IEEE Conference on Decision and Control, 2021, pp. 5073–5079.
    Paper
  19. A. J. Thorpe, K. R. Ortiz, and M. M. K. Oishi, “Learning approximate forward reachable sets using separating kernels,” in Proceedings of the 3rd Conference on Learning for Dynamics and Control, vol. 144, PMLR, Jul. 2021, pp. 201–212.
    Paper
  20. A. J. Thorpe and M. M. K. Oishi, “Stochastic optimal control via Hilbert space embeddings of distributions,” in 2021 60th IEEE Conference on Decision and Control, 2021, pp. 904–911.
    Paper
  21. A. Abate, H. Blom, M. Bouissou, et al., “ARCH-COMP21 category report: Stochastic models,” in 8th International Workshop on Applied Verification of Continuous and Hybrid Systems (ARCH21), ser. EPiC Series in Computing, United Kingdom, Dec. 2021, pp. 55–89.
    Paper
  22. A. J. Thorpe, J. A. Gonzales, and M. M. K. Oishi, “Data-driven stochastic optimal control using kernel gradients,” in 2023 American Control Conference (ACC), 2023, pp. 2548–2553.
    Paper
  23. A. J. Thorpe, “Refining human-centered autonomy using side information,” in 14th ACM/IEEE International Conference on Cyber-Physical Systems, Humans in Cyber-Physical Systems Workshop, 2023.
    Paper
  24. A. J. Thorpe, C. L. Arrington, and J. R. Pillars, “Additively manufactured electrochemical plating enclosures,” in ECS Meeting Abstracts, IOP Publishing, 2018, p. 857.

Talks

  1. A. J. Thorpe, “Data-Driven Stochastic Optimal Control Using Hilbert Space Embeddings of Distributions,” Dissertation Defense, University of New Mexico, 2023
    Paper Slides
  2. A. J. Thorpe, “Learning for Autonomy: From Operators to Policies to Distributions,” CU Boulder, 2025
    Slides
  3. A. J. Thorpe, “Stochastic Optimal Control & Safety Via Kernel Embeddings,” University of Texas at Austin, 2022
    Slides
  4. A. J. Thorpe, “Stochastic Optimal Control & Safety Via Kernel Embeddings: A Data-Driven Approach,” Weierstrass Institute for Applied Analysis and Stochastics in Berlin, Germany, 2022
    Slides
  5. A. J. Thorpe, “LP Solutions for Stochastic Optimal Control Problems via Hilbert Space Embeddings of Distributions,” NASA ULI Seminar Series, Stanford University, 2022
    Video Slides